Giải câu 1 trang 125 toán VNEN 9 tập 1

E. HOẠT ĐỘNG LUYỆN TẬP

Câu 1: Trang 125 sách VNEN 9 tập 1

Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với M thuộc (O) và N thuộc (O'). Từ M và N kẻ các dường vuông góc với OO' chúng cắt (O) và (O') thứ tự tại P và Q.

a) Tứ giác MNQP là hình gì? Vì sao?

b) Chứng minh rằng PQ là tiếp tuyến chung của hai đường tròn (O) và (O').

c) So sánh MN + PQ và MP + NQ.

Bài làm:

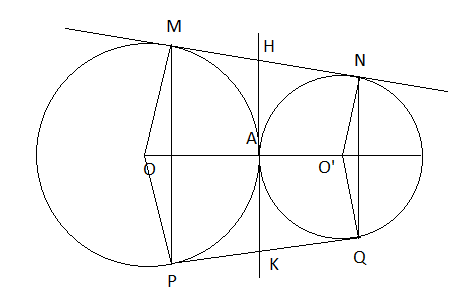
a) Ta có: MP//NQ nên tứ giác MNQP là hình thang

Mặt khác OO' vuông góc với MP và NQ tại trung điểm của MP và NQ nên tứ giác MNQP là hình thang cân

b) OMP có OM = OP nên OMP là tam giác cân

$\widehat{OPM}$ = $\widehat{OMP}$

Tứ giác MNQP là hình thang cân nên = $\widehat{PMN}$

$\widehat{OPM}$ + $\widehat{MPQ}$ = $\widehat{OMP}$ + $\widehat{PMN}$ = ${90}^{\circ }$ $\widehat{OPQ}$ = ${90}^{\circ }$ hay OP $\perp$ PQ

Tương tự ta chứng minh được O'Q PQ

Suy ra PQ là tiếp tuyến chung của (O) và (O').

c) Kẻ tiếp tuyến chung của hai đường tròn tại A cắt MN tại H, cắt PQ tại K

Trong đường tròn (O), theo tính chất hai đường trung tuyến cắt nhau, ta có: MH = AH = HN MN = 2AH

Trong đường tròn (O'), theo tính chất hai đường trung tuyến cắt nhau, ta có: PK = AK = KQ PQ = 2AK

MN + PQ = 2(AH + AK) = 2HK (1)

Mặt khác HK là đương trung bình của hình thang cân MNQP nên

HK = $\Rightarrow$ MP + NQ = 2HK (2)

Từ (1) và (2) suy ra MN + PQ = MP + NQ.