Giải câu 1 trang 70 toán VNEN 8 tập 1
Câu 1: Trang 70 toán VNEN 8 tập 1
Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh rằng MI = IK = KN.
Bài làm:
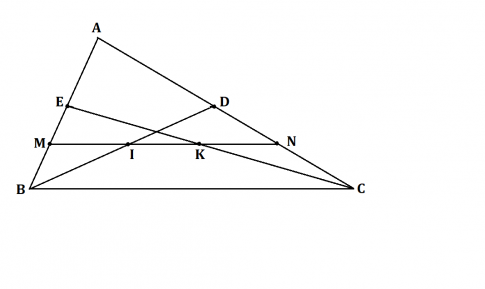
Đặt BC = a.
Vì tam giác ABC có AE = EB, AD = DC nên ED là đường trung bình, do đó ED // BC và ED = ![]() = $\frac{a}{2}$.
= $\frac{a}{2}$.
Do MN là đường trung bình của hình thang BEDC nên MN // ED // BC.
Tam giác BED có BM = ME, MI // ED nên MI là đường trung bình, MI = ![]() = $\frac{a}{4}$.
= $\frac{a}{4}$.
Tam giác CED có CN = ND, NK // ED nên NK là đường trung bình, NK = ![]() = $\frac{a}{4}$.
= $\frac{a}{4}$.
Tam giác EBC có EM = MB, MK // BC nên MK là đường trung bình, MK = ![]() = $\frac{a}{2}$.
= $\frac{a}{2}$.
Suy ra IK = MK – MI = ![]() - $\frac{a}{4}$ = $\frac{a}{4}$.
- $\frac{a}{4}$ = $\frac{a}{4}$.
Vậy MI = IK = KN.
Xem thêm bài viết khác
- Giải câu 1 trang 54 toán VNEN 8 tập 1
- Giải câu 1 trang 65 toán VNEN 8 tập 1
- Giải câu 4 trang 145 toán VNEN 8 tập 1
- Giải câu 2 trang 22 toán VNEN 8 tập 1
- Giải câu 3 trang 9 toán VNEN 8 tập 1
- Giải câu 3 trang 80 toán VNEN 8 tập 1
- Giải câu 1 trang 49 toán VNEN 8 tập 1
- Giải câu 1 trang 89 toán VNEN 8 tập 1
- Giải câu 1 trang 9 toán VNEN 8 tập 1
- Giải câu 3 trang 22 toán VNEN 8 tập 1
- Giải câu 2 trang 59 toán VNEN 8 tập 1 trắc nghiệm
- Giải VNEN toán 8 bài 2: Diện tích hình tam giác











