Giải câu 1 trang 96 toán VNEN 9 tập 1

C. HOẠT ĐỘNG LUYỆN TẬP

Câu 1: Trang 96 sách VNEN 9 tập 1

Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Gọi E và F theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng: OE = OF và CF = DE.

Bài làm:

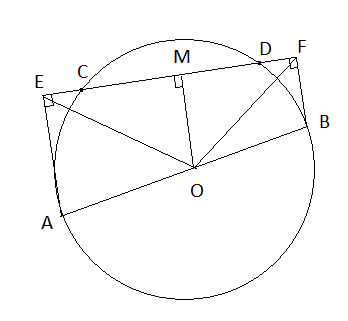
Kẻ OM CD

* Ta có AE//OM//BF (cùng CD)

Theo định lý Ta-lét ta được: = $\frac{BO}{OA}$

Mà OA = OB nên FM = ME

Xét OEF có M là trung điểm EF và OM $\perp $ EF $\Rightarrow $ OEF cân $\Rightarrow $ OE = OF (đpcm).

* Ta có: ME = MF

MC = MD

ME - MC = MF - MD

CE = DF

Ta có: DC + CE = CD + DF CF = DE (đpcm).