Giải câu 2 trang 97 toán VNEN 7 tập 1

Câu 2: Trang 97 toán VNEN 7 tập 1

Luyện tập

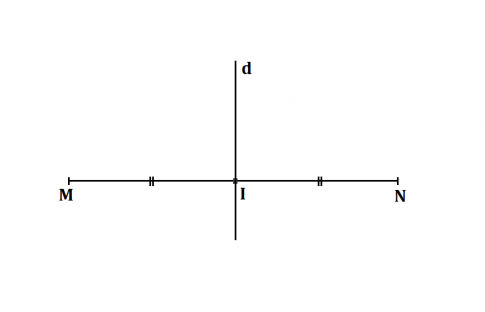
a) Vẽ đoạn thẳng MN = 5cm. Vẽ đường trung trực của đoạn thẳng MN.

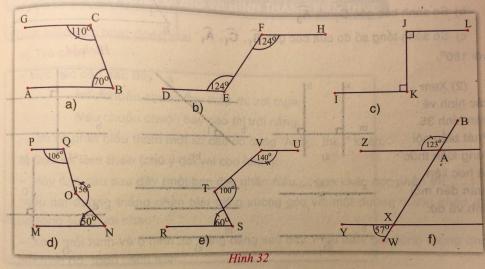
b) Cho hình 32, trong mỗi trường hợp hình vẽ có hai đường thẳng song song với nhau. Tìm ra và kể tên hai đường thẳng song song với nhau đó. Giải thích các hiểu của em.

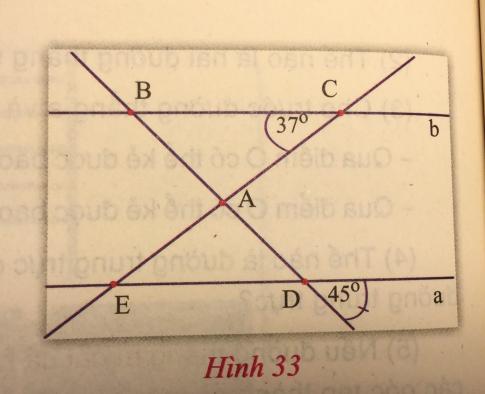
c) Cho hình 33, biết a // b.

- Tìm các cặp góc bằng nhau có trên hình đó.

- Tìm số đo của các góc: ; $\widehat{AED}$.

Bài làm:

a)

b)

Trường hợp a: Hai đường thẳng song song là AB và GC vì hai đường thẳng này có hai góc trong cùng phía bù nhau.

Trường hợp b: Hai đường thẳng song song là FH và DE vì hai đường thẳng này có hai so le trong bằng nhau.

Trường hợp c: Hai đường thẳng song song là IK và JL vì hai đường thẳng này cùng vuông góc với đường thẳng thứ ba là JK.

Trường hợp d:

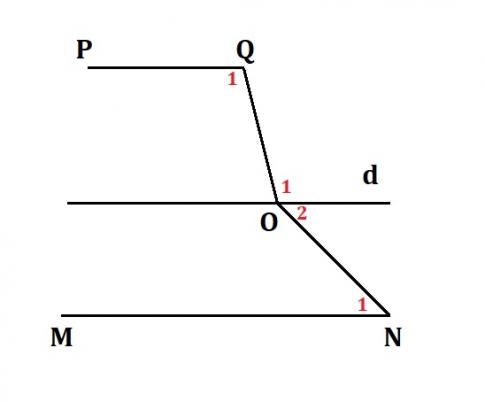
Qua điểm O, kẻ đường thẳng d song song với PQ (1).

Vì PQ // d nên ta có: = $\widehat{O_1}$ (so le trong) $\Rightarrow$ $\widehat{O_1}$ = 106${}^0$.

Mà + $\widehat{O_2}$ = 156${}^0$ $\Rightarrow$ $\widehat{O_2}$ = 156${}^0$ - = 156${}^0$ - 106${}^0$ = 50${}^0$.

Lại có: = $\widehat{N_1}$ = 50${}^0$ và hai góc này ở vị trí so le trong nên suy ra d // MN (2).

Từ (1) và (2) suy ra PQ // MN.

Trường hợp e:

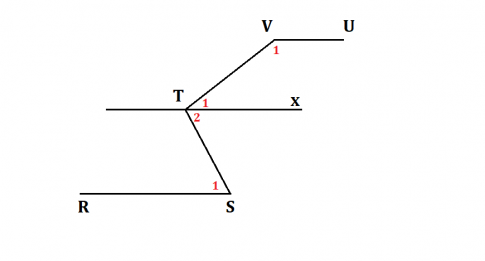
Qua điểm T kẻ đường thẳng x song song với RS. (1)

Ta có: RS // x nên = $\widehat{T_2}$ (so le trong) $\Rightarrow$ $\widehat{T_1}$ = 60${}^0$.

Mà + $\widehat{T_2}$ = 100${}^0$ $\Rightarrow$ = 156${}^0$ - $\widehat{T_2}$ = 100${}^0$ - 60${}^0$ = 40${}^0$.

Lại có: + $\widehat{V_1}$ = 180${}^0$ và hai góc này ở vị trí trong cùng phía nên suy ra x // VU. (2)

Từ (1) và (2) suy ra RS // VU.

Trường hợp f:

Ta có: + $\widehat{ZAX}$ = 180${}^0$ (hai góc kề bù) $\Rightarrow$ $\widehat{ZAX}$ = 180${}^0$ - = 180${}^0$ - 123${}^0$ = 57${}^0$;

Vì = $\widehat{YXW}$ = 57${}^0$ và hai góc ở vị trí đồng vị nên AZ // WY.

c)

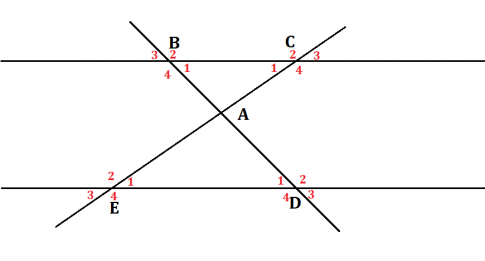
- Các cặp góc bằng nhau là:

= $\widehat{D_1}$; $\widehat{B_4}$ = $\widehat{D_2}$; = $\widehat{D_3}$;

= $\widehat{D_2}$; $\widehat{B_4}$ = $\widehat{D_4}$; $\widehat{B_3}$ = $\widehat{D_1}$;

= $\widehat{E_3}$; $\widehat{E_4}$ = $\widehat{C_4}$; $\widehat{C_3}$ = $\widehat{E_1}$;

= $\widehat{E_2}$; $\widehat{E_2}$ = $\widehat{C_4}$; $\widehat{C_1}$ = $\widehat{E_1}$;

= $\widehat{EAD}$; $\widehat{BAE}$ = $\widehat{CAD}$.

- Tính :

Vì a // b nên = $\widehat{D_3}$ (hai góc đồng vị) $\Rightarrow$ = $\widehat{D_3}$ = 45${}^0$.

- Tính :

Vì a // b nên = $\widehat{C_1}$ (hai góc so le trong) $\Rightarrow$ = $\widehat{C_1}$ = 37${}^0$.