Giải câu 4 trang 129 sách toán VNEN lớp 7 tập 1

Câu 4: Trang 129 sách toán VNEN lớp 7 tập 1

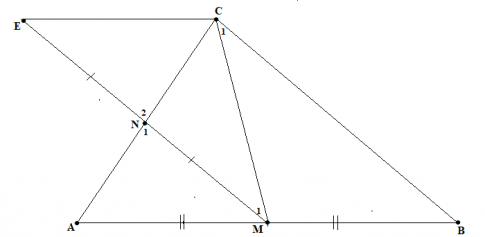
Cho tam giác ABC, M là trung điểm của AB. Từ M kẻ đường thẳng song song với BC cắt AC tại N. Lấy E trên đường thẳng MN sao cho N là trung điểm của ME. Chứng minh rằng:

a) và CE = MB.

b) và MN // BC; MN = $\frac{1}{2}$BC.

Bài làm:

a) Do MN // BC mà M là trung điểm của AB nên N là trung điểm của AC (theo tính chất của đường thẳng song song).

Xét và $\bigtriangleup CEN$ có:

NM = NE (giả thiết);

(hai góc đối đỉnh);

AN = NC (chứng minh trên);

$\bigtriangleup AMN = \bigtriangleup CEN$ (c.g.c) (đpcm);

AM = CE

Lại có: AM = MB (giả thiết) nên CE = BM (đpcm);

b)

• Chứng minh:

Xét và $\bigtriangleup ECM$ có:

CM chung;

(hai góc đối đỉnh);

CE = MB (chứng minh trên);

$\bigtriangleup BMC = \bigtriangleup ECM$ (c.g.c) (đpcm);

• Chứng minh: MN // BC; MN = BC.

+ Theo giả thiết: MN // BC (đpcm);

+ Ta có: EM = CB (hai cạnh tương ứng) mà MN = NE = (theo cách vẽ);

Suy ra: MN = BC (đpcm)