Giải câu 4 trang 83 sách toán VNEN lớp 8 tập 2

Câu 4: Trang 83 sách VNEN 8 tập 2

Hình thang ABCD (AB // CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.

Bài làm:

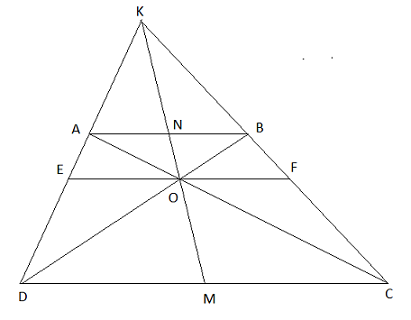
Tứ giác ABCD là hình thang nên AB//CD

Gọi N, M lần lượt là giao điểm của KO với AB,CD.

Áp dụng định lý talet ta có:

= $\frac{NB}{MC}$ = $\frac{KN}{KM}$ = $\frac{AN + NB}{DM + MC}$ = $\frac{AB}{DC}$ (1)

Vì AB // DC nên = $\frac{AO}{OC}$

Vì AN // MC nên = $\frac{AN}{MC}$

$\frac{AB}{DC}$ = $\frac{AN}{MC}$ (2)

Từ (1) và (2) ta được: = $\frac{AN}{MC}$ hay MD = MC

Tương tự ta được: NA = NB

Vậy OK đi qua trung điểm của AB và CD.