Giải câu 6 trang 80 toán VNEN 9 tập 2

Câu 6: Trang 80 toán VNEN 9 tập 2

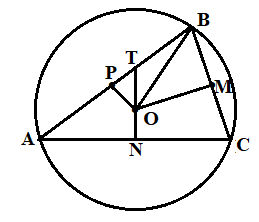
Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Gọi (O) là đường tròn đi qua các đỉnh của tam giác ABC. Gọi T là giao điểm của ON và AB, biết P thuộc đoạn BP.

a) So sánh hai cung nhỏ BC và BA.

b) Chứng minh rằng OM > OP

Bài làm:

a) Ta có: N là trung điểm của AC, O là tâm đường tròn ngoại tiếp tam giác ABC (Đường tròn đi qua ba đỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó)

ON đi qua điểm chính giữa cung AC.

Theo đề bài, A và B nằm ở hai phía của đường thẳng ON

AB > BC cung nhỏ AB > cung nhỏ BC (mối liên hệ giữa dây và cung).

b)

Ta có: N là trung điểm của AC, P là trung điểm của AB; N là trung điểm của AC.

Theo bài 5,

Xét các tam giác BOP và BOM vuông tại P và M:

(Định lý Pytago)

(Định lý Pytago)

Lại có: ; $BM = \frac{1}{2} BC$

Mà AB > BC

hay OP < OM (đpcm)