Giải câu 3 trang 126 toán VNEN 8 tập 1

Câu 3: Trang 126 toán VNEN 8 tập 1

a) Cho tam giác đều cạnh a. Hãy tính diện tích tam giác này theo a.

b) Cho tam giác cân có cạnh đáy là a, cạnh bên là b. Hãy tính diện tích tam giác này theo a và b.

Bài làm:

a)

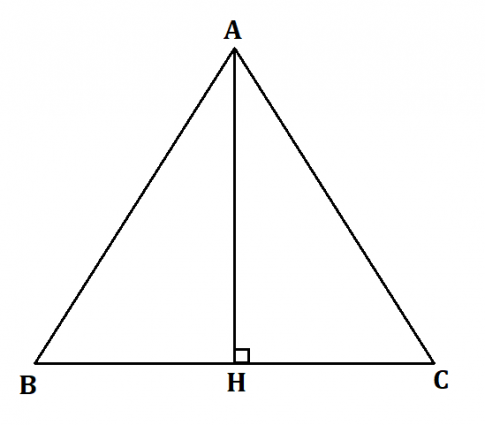
Xét tam giác ABC đều có cạnh bằng a, đường cao AH.

Vì tam giác ABC đều nên đường cao AH đồng thời là đường trung tuyến BH = $\frac{BC}{2}$ = $\frac{a}{2}$.

Áp dụng định lí Pi-ta-go vào tam giác AHB vuông tại H, ta có:

AH = = $\sqrt{a^{2} – (\frac{a}{2})^{2}}$ = $\frac{a\sqrt{3}}{2}$.

Như vậy: S = $\frac{AH.BC}{2}$ = $\frac{1}{2}$.$\frac{a\sqrt{3}}{2}$.a = $\frac{a^{2}\sqrt{3}}{4}$.

b)

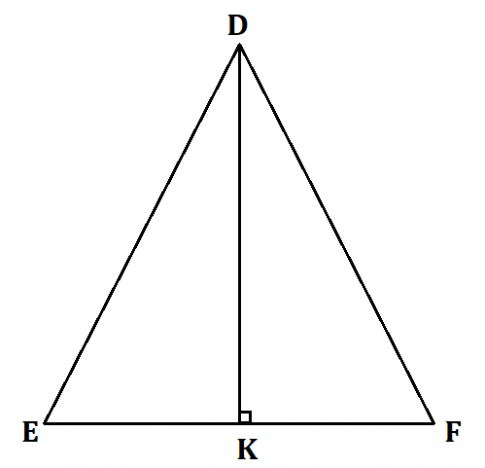
Xét tam giác DEF cân tại D có cạnh đáy bằng a, cạnh bên bằng b, đường cao DK.

Vì tam giác DEF cân tại D nên đường cao DK đồng thời là đường trung tuyến DK = $\frac{EF}{2}$ = $\frac{a}{2}$.

Áp dụng định lí Pi-ta-go vào tam giác DKE vuông tại K, ta có:

DK = = $\sqrt{b^{2} – (\frac{a}{2})^{2}}$ = $\sqrt{b^{2} – \frac{a^{2}}{4}}$.

Như vậy: S = $\frac{DK.EF}{2}$ = $\frac{1}{2}$.($\sqrt{b^{2} – \frac{a^{2}}{4}}$).b = $\frac{b\sqrt{b^{2} – \frac{a^{2}}{4}}}{2}$.