Giải câu 4 trang 111 toán VNEN 9 tập 2

Câu 4: Trang 111 toán VNEN 9 tập 2

Chứng minh rằng: Nếu một tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứ hai đỉnh còn lại dưới một góc vuông thì nó là tứ giác nội tiếp.

Bài làm:

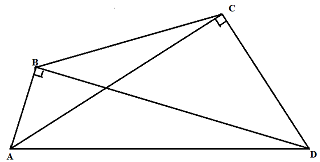
Giả sử, tứ giác ABCD có đỉnh B và đỉnh C cùng nhìn cạnh AD dưới một góc , ta cần chứng minh ABCD nội tiếp được.

Xét tam giác ABD vuông tại B nên tam giác ABC nội tiếp đường tròn (O) đường kính AD.

Tam giác ACD vuông tại C nên tam giác ABC nội tiếp đường tròn (O') đường kính AD.

Hai đường tròn (O) và (O') cùng có đường kính là AD nên trùng nhau, do đó A, B, C, D cùng thuộc một đường tròn hay ABCD nội tiếp được