Giải câu 44 bài: Ôn tập chương II Đa giác. Diện tích đa giác sgk Toán 8 tập 1 Trang 133

Câu 44 : Trang 133 sgk toán 8 tập 1

Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO.

Bài làm:

Từ O lẻ đường thẳng d vuông góc với AB ở H₁, cắt CD ở H₂.

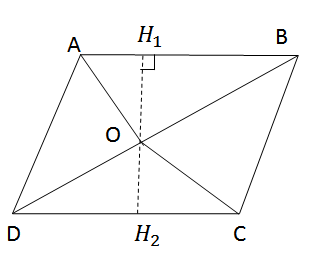
Ta có OH₁ ⊥ AB mà AB // CD => OH₂ ⊥ CD

Tổng diện tích hai tam giác ABO và CDO là:

=

mà là chiều cao của hình bình hành ABCD ứng với đáy AB.

=> ( 1)

Chứng minh tương tự ta được: (2)

Từ (1) và (2) suy ra :

(đpcm)