Giải câu 5 trang 98 toán VNEN 8 tập 1

Câu 5: Trang 98 toán VNEN 8 tập 1

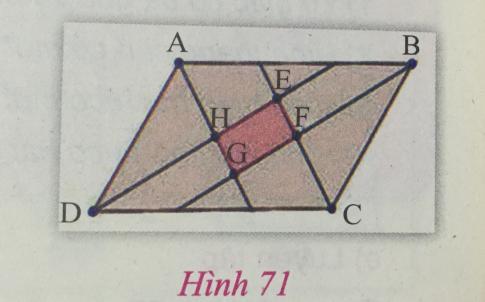
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 71. Chứng minh rằng EFGH là hình chữ nhật.

Bài làm:

Ta có: $\widehat{A_{1}}$ = $\hat{J_{1}}$ (so le trong)

Mà $\widehat{A_{1}}$ = $\hat{C_{1}}$ (đường phân giác của hai góc đối trong hình bình hành)

$\Rightarrow$ $\hat{J_{1}}$ = $\hat{C_{1}}$ và hai góc này lại ở vị trí đồng vị

$\Rightarrow$ AJ // CE hay HG // EF. (1)

Có $\widehat{D_{1}}$ = $\hat{B_{1}}$ (đường phân giác của hai góc đối trong hình bình hành)

Mà $\widehat{B_{1}}$ = $\hat{I_{1}}$ (so le trong)

$\Rightarrow$ $\hat{D_{1}}$ = $\hat{I_{1}}$ và hai góc này lại ở vị trí đồng vị

$\Rightarrow$ DE // BI hay HE // GF. (2)

Từ (1) và (2) $\Rightarrow$ HEFG là hình bình hành. (*)

Ta có: $\widehat{J_{1}}$ = $\hat{A_{1}}$

Mà $\widehat{A_{1}}$ + $\widehat{D_{1}}$ = 90 $^{0}$ (phân giác của hai góc kề bù trong hình bình hành)

$\Rightarrow$ $\hat{J_{1}}$ + $\widehat{D_{1}}$ = 90 $^{0}$

$\Rightarrow$ $\hat{D H J}$ = 90 $^{0}$ hay $\hat{G H E}$ = 90 $^{0}$ . (**)

Từ (*) và (**) $\Rightarrow$ HEFG là hình chữ nhật (đpcm).

Cập nhật: 07/09/2021

Xem thêm bài viết khác