Giải câu 4 trang 131 toán VNEN 8 tập 1

Câu 4: Trang 131 toán VNEN 8 tập 1

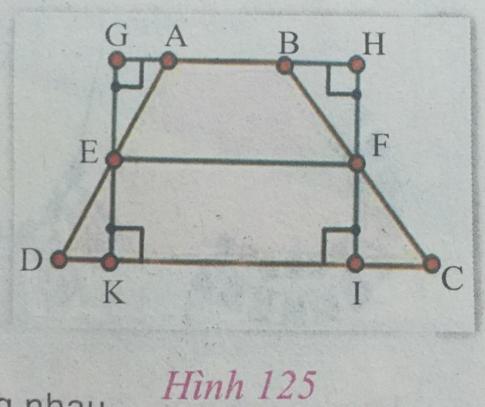
Bạn Minh đã vẽ hình thang ABCD (AB // CD, AB < CD) (hình 125). Gọi E và F tương ứng là trung điểm của AD và BC; gọi K và I tương ứng là hình chiếu vuông góc của E và F trên đường thẳng CD; gọi G và H tương ứng là hình chiếu vuông góc của E và F trên đường thẳng AB.

Bạn Minh cho rằng hai tam giác vuông EGA và EKD bằng nhau; hai tam giác vuông FHB và FIC bằng nhau.

Từ đó suy ra: S = S${}_{GHIK}$ = KI.GK = EF.GK = $\frac{1}{2}$(AB + CD).GK.

Theo em, bạn Minh làm đúng hay sai? Vì sao?

Có thể xem đó là cách khác để tìm ra công thức tính diện tích hình thang hay không?

Bài làm:

Xét EGA vuông tại G và EKD vuông tại K, có:

= $\widehat{DEK}$

AE = DE (E là trung điểm AD)

$\mathrm{\Delta }$EGA = $\mathrm{\Delta }$EKD (cạnh huyền – góc nhọn)

Chứng minh tương tự, ta cũng có FHB = FIC.

Như vậy:

S = S${}_{DEK}$ + S${}_{CFI}$ + S${}_{ABFIKE}$ = S${}_{GAE}$ + S${}_{FHB}$ + S${}_{ABFIKE}$ = S${}_{GHIK}$ = KI.GK = EF.GK (vì GHIK là hình chữ nhật do có 4 góc vuông). (1)

Lại có: EF là đường trung bình của hình thang ABCD nên EF = (AB + CD). (2)

Từ (1) và (2) S${}_{ABCD}$ = S${}_{GHIK}$ = KI.GK = EF.GK = $\frac{1}{2}$(AB + CD).GK.

Vậy, bạn Minh làm đúng. Có thể xem đó là cách khác để tìm ra công thức tính diện tích hình thang.