Giải Câu 6 Bài 2: Hai đường thẳng vuông góc

Câu 6: Trang 98 - SGK Hình học 11

Trong không gian cho hai hình vuông và $AB{C}^{\prime }{D}^{\prime }$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm $O$ và $O^{\prime }$. Chứng minh rằng $AB\perp O{O}^{\prime }$ và tứ giác $CD{D}^{\prime }{C}^{\prime }$ là hình chữ nhật.

Bài làm:

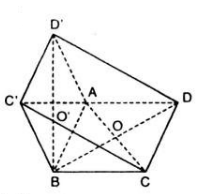
Gọi cạnh của hai hình vuông bằng nhau ABCD và ABC'D" là .

• Ta có:

.

Vậy .

• Ta có:

.

=> (1)

• Mặt khác: song song và bằng $C^{\prime }{D}^{\prime }$ (do ABCD và ABC'D' là hai hình vuông bằng nhau)

=> là hình bình hành (2)

Từ (1) (2) => là hình chữ nhật.