Dạng 2: Lăng trụ đứng có góc giữa hai mặt phẳng

Dạng 2: Lăng trụ đứng có góc giữa hai mặt phẳng

Bài làm:

I.Phương pháp giải

Từ góc giữa hai mặt phẳng ta suy ra được góc giữa hai đường thẳng qua đó ta tìm được chiều cao và diện tích đáy từ đó tính được thể tích khối lăng trụ.

II,Bài tập vận dụng

Bài tập 1: Cho lăng trụ đứng tam giác có đáy ABC là tam giác vuông cân tại B với BA = BC = a, biết $(A^{{}^{\prime }}BC)$ hợp với đáy (ABC) một góc ${60}^{\circ }$. Tính thể tích lăng trụ.

Bài giải

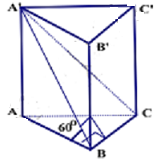
Ta có :

Mà và (ABC) cắt nhau tại BC, $BC\perp A^{{}^{\prime }}B$, $AB\perp BC$ nên $\widehat{((A^{{}^{\prime }}BC),(ABC))}=\widehat{(AB,A^{{}^{\prime }}B)}=\widehat{AB{A}^{{}^{\prime }}}={30}^{\circ }$.

Xét tam giác vuông tại A có: $A{A}^{{}^{\prime }}=ABtan{.60}^{\circ }=a\sqrt{3}$

.

Bài tập 2: Cho lăng trụ tứ giác đều ' có cạnh đáy a và mặt phẳng $(BD{C}^{{}^{\prime }})$ hợp với đáy một góc ${60}^{\circ }$. Tính thể tich khối hộp chữ nhật.

Bài giải

Gọi O là tâm của đáy ABCD. Ta có ABCD là tâm của hình vuông nên .

Mà:

( định lí 3 đường vuông góc).

Do đó .

Xét tam giác vuông tại C: $C{C}^{{}^{\prime }}$=OC.tan.${60}^{\circ }$=$\frac{a\sqrt{6}}{2}$.

Vậy . $C{C}^{{}^{\prime }}$= $a^2.\frac{a\sqrt{6}}{2}=\frac{a^3\sqrt{6}}{2}$