Giải Câu 1 Bài 3: Phương trình đường elip sgk Hình học 10 Trang 88

Câu 1: Trang 88 - SGK Hình học 10

Xác đinh độ dài các trục, tọa độ tiêu điểm , tọa độ các đỉnh và vẽ các elip có phương trình sau:

a) $\frac{x^{2}}{25} + \frac{y^{2}}{9}= 1$

b) $4x^2+ 9y^2= 1$

c) $4x^2+ 9y^2= 36$

Bài làm:

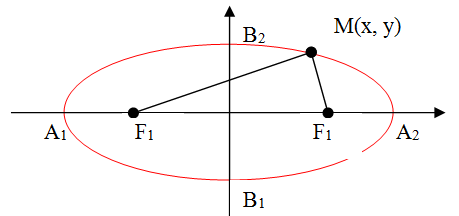
Giải Câu 1 Bài 3: Phương trình đường elip - sgk Hình học 10 Trang 88

a) Ta có: $a^2= 25 \Rightarrow a = 5$ độ dài trục lớn $2 a = 10$

$b^2= 9 \Rightarrow b = 3$ độ dài trục nhỏ $2 a = 6$

$c^2= a^2– b^2= 25 - 9 = 16 \Rightarrow c = 4$

Vậy hai tiêu điểm là: $F_1(-4 ; 0)$ và $F_{2} (4; 0)$

Tọa độ các đỉnh: $A_1(-5; 0), A_2(5; 0), B_1(0; -3), B_2(0; 3)$ .

$4x^2+ 9y^2= 1\Leftrightarrow \frac{x^{2}}{\frac{1}{4}} + \frac{y^{2}}{\frac{1}{9}} = 1$

$a^2 =\frac{1}{4}\Rightarrow a = \frac{1}{2}$ $\Rightarrow$ độ dài trục lớn $2 a = 1$

$b^2= \frac{1}{9}\Rightarrow b = \frac{1}{3}$ $\Rightarrow$ độ dài trục nhỏ $2 b = \frac{2}{3}$

$c^2= a^2– b^2= \frac{1}{}4- \frac{1}{9} = \frac{5}{36}\Rightarrow c = \frac{\sqrt{5}}{6}$

Vậy hai tiêu điểm là: $F_1(-\frac{\sqrt{5}}{6} ; 0)$ và $F_{2} (\frac{\sqrt{5}}{6}; 0)$

Tọa độ các đỉnh: $A_1(-\frac{1}{2}; 0), A_2(\frac{1}{2}; 0),B_1(0; -\frac{1}{3} ), B_2(0; \frac{1}{3} )$ .

c) Chia $2$ vế của phương trình cho $36$ ta được: $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$

Từ đây suy ra: $2a = 6, 2b = 4, c = \sqrt5$

Suy ra tọa độ hai tiêu điểm là: $F_1(-\sqrt5 ; 0)$ và $F_{2} (\sqrt{5}; 0)$

Tọa độ các đỉnh là: $A_1(-3; 0), A_2(3; 0), B_1(0; -2), B_2(0; 2)$ .

Cập nhật: 07/09/2021

Xem thêm bài viết khác