Giải câu 10 bài: Mặt cầu

Câu 10: Trang 49 - sgk hình học 12

Cho hình chóp S.ABC có bốn đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc.

Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.

Bài làm:

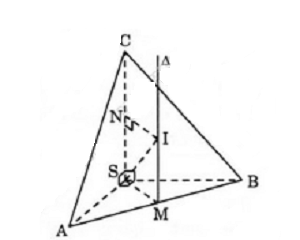
Hướng dẫn giải câu 10 bài Mặt cầu

Gọi H là tâm đường tròn ngoại tiếp tam giác SBC

=> HB = HC

Kẻ $Ht\perp mp(SBC)$ => Ht // SA.

Mặt khác, ta có: $OS=OA=OB=OC=$

=> O là tâm mặt cầu ngoại tiếp hình chóp S.ABC

=> Bán kính mặt cầu đó là: $R=OS=\sqrt{OH^{2}+SH^{2}}$

Mà $OH=IS=\frac{SA}{2}=\frac{a}{2}$

=> $SH=\frac{BC}{2}=\frac{\sqrt{SB^{2}+SC^{2}}}{2}=\frac{b^{2}+c^{2}}{2}$

=> $R=\frac{a^{2}+b^{2}+c^{2}}{2}$

Vậy bán kính là $R=\frac{a^{2}+b^{2}+c^{2}}{2}$

Diện tích mặt cầu là:

$S=4\prod R^{2}=\prod (a^{2}+b^{2}+c^{2})$

Thể tích khối cầu là:

$V=\frac{4}{3}\prod R^{3}=\frac{1}{6}\prod\sqrt{(a^{2}+b^{2}+c^{2})^{3}}$

Cập nhật: 07/09/2021

Xem thêm bài viết khác