Giải câu 27 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung sgk Toán 9 tập 2 Trang 79

Câu 27: Trang 79 – SGK Toán 9 tập 2

Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh = $\widehat{PBT}$

Bài làm:

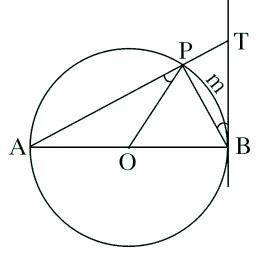
Ta có: BT là tiếp tuyến của đường tròn (O) tại B, PB là dây cung

=> là góc tạo bởi tia tiếp tuyến và dây cung của (O)

=> = $\frac{1}{2}$ sđ cung PmB. (1)

Lại có: là góc nội tiếp chắn cung PmB

=> = $\frac{1}{2}$ sđ cung PmB. (2)

Từ (1) (2) suy ra = $\widehat{PAO}$ (=$\frac{1}{2}$ sđ cung PmB) (3)

Tam giác OAP cân tại O (OA = OP = R) => = $\widehat{PAO}$ (4)

Từ (3), (4) suy ra = $\widehat{PBT}$ (đpcm)