Giải Câu 3 Bài 5: Khoảng cách

Câu 3: Trang 119 - SGK Hình học 11

Cho hình lập phương cạnh \(a\). Chứng minh rằng các khoảng cách từ các điểm \(B, C, D, A', B', D'\) đến đường chéo \(AC'\) đều bằng nhau. Tính khoảng cách đó.

Bài làm:

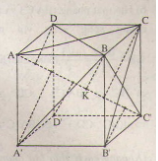
Gọi là hình chiếu của \(B\) trên \(AC'\).

Xét tam giác vuông tại \(B\), ta có:

=>

Ta có:

Do đó khoảng cách từ tới \(AC'\) đều bằng \( \frac{a\sqrt{6}}{3}\) vì chúng đều là chiều cao của các tam giác vuông bằng nhau.