Giải Câu 2 Bài Vecto trong không gian

Câu 2: Trang 91 - SGK Hình học 11

Cho hình hộp . Chứng minh rằng:

a) + $\overrightarrow{B^{\prime }{C}^{\prime }}$ + $\overrightarrow{D{D}^{\prime }}$ = $\overrightarrow{A{C}^{\prime }}$;

b) - $\overrightarrow{D^{\prime }D}$ - $\overrightarrow{B^{\prime }{D}^{\prime }}$ = $\overrightarrow{B{B}^{\prime }}$;

c) + $\overrightarrow{B{A}^{\prime }}$ + $\overrightarrow{DB}$ + $\overrightarrow{C^{\prime }D}$ = $\overrightarrow{0}$.

Bài làm:

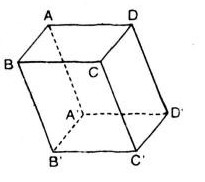
a) Ta có: , $\overrightarrow{D{D}^{\prime }}=\overrightarrow{C{C}^{\prime }}$

=> + $\overrightarrow{B^{\prime }{C}^{\prime }}$ + $\overrightarrow{D{D}^{\prime }}$ = + $\overrightarrow{BC}$ + $\overrightarrow{C{C}^{\prime }}$ = $\overrightarrow{A{C}^{\prime }}$

b) Ta có: , $\overrightarrow{B^{\prime }{D}^{\prime }}=-\overrightarrow{D^{\prime }{B}^{\prime }}$

=> - $\overrightarrow{D^{\prime }D}$ - $\overrightarrow{B^{\prime }{D}^{\prime }}$ = + $\overrightarrow{D{D}^{\prime }}$ + $\overrightarrow{D^{\prime }{B}^{\prime }}$ = $\overrightarrow{B{B}^{\prime }}$

c) Ta có: , $\overrightarrow{DB}=\overrightarrow{D^{\prime }{B}^{\prime }}$, $\overrightarrow{C^{\prime }D}=\overrightarrow{B^{\prime }A}$

=> + $\overrightarrow{B{A}^{\prime }}$ + $\overrightarrow{DB}$ + $\overrightarrow{C^{\prime }D}$ = + $\overrightarrow{C{D}^{\prime }}$ + $\overrightarrow{D^{\prime }{B}^{\prime }}$ + $\overrightarrow{B^{\prime }A}$ = $\overrightarrow{0}$.