Giải Câu 1 Bài 2: Hai đường thẳng vuông góc

1 Đánh giá

Câu 1: Trang 97 - SGK Hình học 11

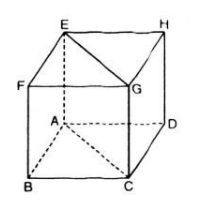
Cho hình lập phương $ABCD.EFGH$ . Hãy xác định góc giữa các cặp vectơ sau đây:

a) $\overrightarrow{AB}$ và $\vec{E G};$

b) $\overrightarrow{AF}$ và $\vec{E G};$

c) $\overrightarrow{EG}$ và $\vec{D H} .$

Bài làm:

Giải Câu 1 Bài 2: Hai đường thẳng vuông góc

a) Góc giữa $\overrightarrow{AB},\overrightarrow{EG}$ .

Ta có: $\overrightarrow{AB}=\overrightarrow{EF}$ => $(\vec{A B}, \vec{E G}) = (\vec{E F}, \vec{E G}) = \hat{F E G}$

Vì $EFGH$ là hình vuông, EG là một đường chéo => $\hat{F E G} = 45^{0}$

Vậy $\left ( \overrightarrow{AB},\overrightarrow{EG} \right )=45^0$ .

b) Góc giữa $\overrightarrow{AF},\overrightarrow{EG}$ .

Ta có: $\overrightarrow{AF}=\overrightarrow{GD}$ => $(\vec{A F}, \vec{E G}) = (\vec{G D}, \vec{E G}) = \hat{E G D}$

Vì $EFGH,CDHG,AEHD$ là các hình vuông bằng nhau lần lượt có các đường chéo $EG,GD,ED$

=> $EG=GD=ED$

=> $\Delta EDG$ là tam giác đều

=> $\widehat{EGD}=60^0$

Vậy $\overrightarrow{AF},\overrightarrow{EG}=60^0$ .

c) Góc giữa $\overrightarrow{AB},\overrightarrow{DH}$ .

Ta có: $\overrightarrow{DH}=\overrightarrow{AE}$ => $(\vec{A B}, \vec{D H}) = (\vec{A B}, \vec{A E}) = \hat{E A B}$

Mà $\widehat{EAB}=90^0$ (do $A E F B$ là hình vuông)

Vậy $\overrightarrow{AB},\overrightarrow{DH}=90^0$ .

lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Toán Hình 11