Giải Câu 6 Bài: Bài tập ôn tập chương 3

1 Đánh giá

Câu 6: Trang 122 - SGK Hình học 11

Cho khối lập phương ABCD.A'B'C'D' cạnh a.

a) Chứng minh BC' vuông góc với mặt phẳng (A'B'CD)

b) Xác định và tính độ dài đoạn vuông góc chung của AB' và BC'

Bài làm:

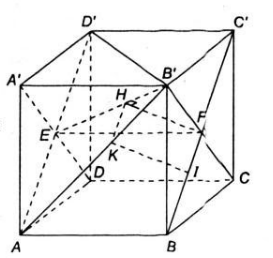
Giải Câu 6 Bài: Bài tập ôn tập chương 3

a) Ta có tứ giác $BCC'B’$ là hình vuông nên

$BC’ ⊥ B’C$ (1)

Mặt khác $A’B’ ⊥ (BCC’B’)$

$⇒ A’B’ ⊥ BC’$ (2)

Từ (1) và (2) suy ra: $BC’⊥ (A’B’C’D')$

b) Do $AD’//BC’$ nên mặt phẳng $(A B^{'} D^{'})$ là mặt phẳng chứa $A B^{'}$ và song song với $B C^{'}$ .

Ta tìm hình chiếu của $BC’$ trên $m p (A B^{'} D^{'})$

Gọi $E, F$ là tâm của các mặt bên $A D D^{'} A^{'}$ và $B C C^{'} B^{'}$

Từ $F$ kẻ $F I ⊥ B^{'} E$ . Ta có $B C^{'} / / A D^{'}$ mà $B C^{'} ⊥ (A^{'} B^{'} C D)$

$⇒ AD’ ⊥ (A’B’CD)$ và $I F \subset (A^{'} B^{'} C D)$

$AD’ ⊥ IF$ (3)

$EB’⊥IF$ (4)

Từ (3) và (4) suy ra : $IF ⊥ (AB’D’)$

Vậy $I$ là hình chiếu của $F$ trên $m p (A B^{'} D^{'})$ . Qua $I$ ta dựng đường thẳng song song với $B C^{'}$ thì đường thẳng này chính là hình chiếu của $B C^{'}$ trên mp $(A B^{'} D^{'})$

Đường thẳng qua $I$ song song với $B C^{'}$ cắt $A B^{'}$ tại $K$ . Qua $K$ kẻ đường thẳng song song với $I F$ , đường này cắt $B C^{'}$ tại $H$ . $K H$ chính là đường vuông góc chung của $A B^{'}$ và $B C^{'}$ . Thật vậy:

${\rm{IF}} \bot (AB'D')$

$\Rightarrow IF ⊥ AB'$ và $K H / / I F$ suy ra $K H ⊥ A B^{'}$

$\begin{matrix} B C^{'} ⊥ (A^{'} B^{'} C D) \\ I F \subset (A^{'} B^{'} C D) \end{matrix}} \Rightarrow \begin{matrix} I F ⊥ B C^{'} \\ K H / / I F \end{matrix}} \Rightarrow K H ⊥ B C^{'}$

Tam giác $EFB’$ vuông góc tại $F$ , $F I$ là đường cao thuộc cạnh huyền nên

${1 \over {I{F^2}}} = {1 \over {FB{'^2}}} + {1 \over {F{E^2}}}$ với

${\begin{matrix} F B^{'} = \frac{a \sqrt{2}}{2} \\ E F = a \end{matrix}$

Ta tính ra: ${\rm{IF}} = {{a\sqrt 3 } \over 3} \Rightarrow KH = {\rm{IF = }}{{a\sqrt 3 } \over 3}$

7 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Toán Hình 11