Giải Câu 3 Bài 4: Hai mặt phẳng vuông góc

Câu 3; Trang 113 - SGK Hình học 11

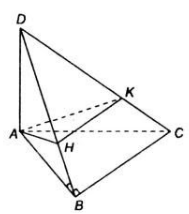
Trong mặt phẳng cho tam giác $ABC$ vuông ở $B$. Một đoạn thẳng $AD$ vuông góc với tại $A$. Chứng minh rằng:

a) là góc giữa hai mặt phẳng $(ABC)$ và $(DBC)$;

b) Mặt phẳng vuông góc với mặt phẳng $(BCD)$;

c) với $H$ và $K$ lần lượt là giao điểm của $DB$ và $DC$ với mặt phẳng $(P)$ đi qua $A$ và vuông góc với $DB$.

Bài làm:

a) Tam giác vuông tại $B(gt)$ nên $AB\mathrm{\perp }BC$ (1)

vuông góc với $(\alpha )$ (gt) nên $AD\mathrm{\perp }BC$ (2)

Từ (1) và (2) ta có:

mà suy ra

Ta có: , , $BC\mathrm{\perp }BD$

=> Góc giữa hai mặt phẳng và $(DBC)$ là (đpcm)

b) Ta có:

$\begin{array}{c}BC\mathrm{\perp }(ABD)(cmt)\hfill \\ BC\subset (BCD)\hfill \end{array}\}\Rightarrow (ABD)\mathrm{\perp }(BCD)$ (đpcm)

c) Ta có: mà đi qua $A$ và vuông góc với $BD$ nên $HK\mathrm{\perp }BD$

Trong có: $HK\mathrm{\perp }BD$ và $BC\mathrm{\perp }BD$ nên suy ra $HK//BC$.