Giải câu 6 bài 2: Cực trị của hàm số

1 Đánh giá

Bài 6: Trang 18 - sgk giải tích 12

Xác định giá trị của tham số m để hàm số $y=\frac{x^{2}+mx+1}{x+m}$ đạt cực đại tại $x=2$.

Bài làm:

Cách 1: TXĐ: $D=\mathbb{R}\setminus \left \{ -m \right \}$

Ta có $y'=\frac{x^{2}+2mx+m^{2}-1}{(x+m)^{2}}=0 \Leftrightarrow \left[ \matrix{x=-m-1\hfill \cr x=-m+1 \hfill \cr} \right.$ .

Do $-m-1<-m+1$ nên ta có bảng biến thiên như sau:

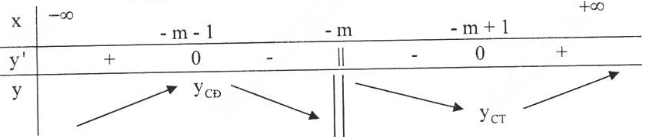
Từ bảng biến thiên ta suy ra hàm số đạt cực đại tại $x=-m-1$

Từ giả thiết ta có $-m-1=2\Leftrightarrow m=-3$ .

Vậy m=-3 thì thỏa mãn đề bài.

Cách 2:

Điều kiện cần: Vì hàm số đạt cực đại tại x=2 nên $y'(2)=0 \Leftrightarrow m^{2}+4m+3=0\Leftrightarrow \left[ \matrix{m=-1\hfill \cr m=-3 \hfill \cr} \right.$

Điều kiện đủ: Thử lại với m=-1, m=-3 thì chỉ có trường hợp m=-3 hàm số đạt cực đại tại x=2.

1 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Giải tích lớp 12