Giải Câu 7 Bài 1: Vecto trong không gian

Câu 7: Trang 92 - SGK Hình học 11

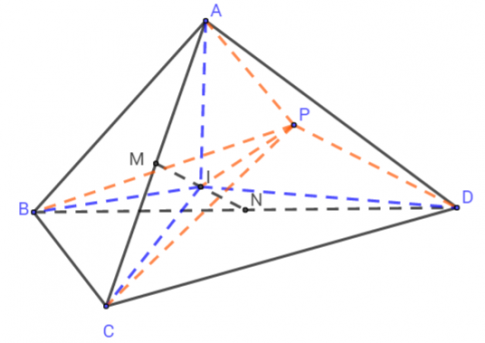
Gọi và \(N\) lần lượt là trung điểm của các cạnh \(AC\) và \(BD\) của tứ diện \(ABCD\). Gọi \(I\) là trung điểm của đoạn thẳng \(MN\) và \(P\) là một điểm bất kì trong không gian. Chứng minh rằng:

a)

b)

Bài làm:

a) (quy tắc đường trung truyến trong tam giác IAC)

(quy tắc đường trung tuyến trong tam giác IBD)

Cộng từng vế ta được :

(do: I là trung điểm của MN nên

b) Theo quy tắc 3 điểm, ta có:

Cộng từng vế ta được:

(1)

Từ a) ta có:

=>

Thay vào (1) có:

\({PI}=\frac{1}{4} (\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}).\)