Đáp án câu 4 đề 8 kiểm tra học kì 2 Toán 9

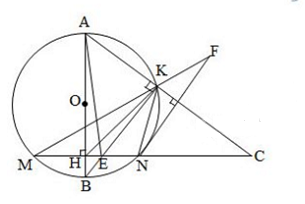
Câu 4(3,5 điểm): Cho đường tròn (O; R), đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (O; R) sao cho đoạn thẳng AC cắt đường tròn (O; R) tại điểm K khác A, hai dây MN và BK cắt nhau ở E.

a) Chứng minh rằng AHEK là tứ giác nội tiếp.

b) Chứng minh CA.CK = CE.CH

c) Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại F. Chứng minh cân.

d, Giả sử KE = KC. Chứng minh OK // MN.

Bài làm:

a, Vì nên $\widehat{AHE} = 90^{\circ}$

Có: (góc nội tiếp chắn nửa đường tròn)

.

Vậy tứ giác AHEK là tứ giác nội tiếp. (Tổng hai góc đối bằng )

b, Xét và $\Delta CHK$ có:

+ chung

+ ( 2 góc nội tiếp cùng chắn cung EK)\

(g.g)

CA.CK = CE.CH

c, Do đường kính AB vuông góc MN nên B là điểm chính giữa cung MN

(1)

Lại có: BK // NF (vì cùng vuông góc với AC) nên (2)

Từ (1) và (2) hay $\widehat{KFN} = \widehat{KNF}$

cân tại K.

d, Ta có:

vuông tại K.

Theo giả thiết ta lại có KE = KC nên tam giác KEC vuông cân tại K

Mặt khác vì cân tại O (do OB = OK = R) nên suy ra vuông cân tại O

OK // MN (cùng vuông góc với AB)