Giải câu 26 Bài 3: Góc nội tiếp sgk Toán 9 tập 2 Trang 76

Câu 26: Trang 76 - SGK Toán 9 tập 2

Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC.Gọi giao điểm của MN và AC là S.Chứng minh SM = SC và SN = SA.

Bài làm:

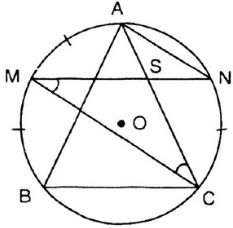
M là điểm chính giữa cung AB (gt) => cung MA = cung MB.

MN // BC => cung MB = cung NC (hai dây song song chắn 2 cung bằng nhau)

Suy ra: cung MA = cung NC (= cung MB)

=> = $\widehat{CMN}$ (định lý về góc nội tiếp chắn cung)

Vậy tam giác SMC là tam giác cân tại S, suy ra SM = SC.

Chứng minh tương tự, ta có tam giác SAN cân tại S => SN = SA