Giải Bài 2: Hai đường thẳng vuông góc

Các đường thẳng có quan hệ vuông góc với nhau như thế nào trong không gian. Để biết chi tiết, KhoaHoc xin chia sẻ với các bạn bài: Hai đường thẳng vuông góc. Với kiến thức trọng tâm và các bài tập có lời giải chi tiết, hi vọng rằng đây sẽ là tài liệu giúp các em học tập tốt hơn.

A. TÓM TẮT KIẾN THỨC

I. TÍCH VÔ HƯỚNG CỦA HAI VECTO TRONG KHÔNG GIAN

1. Góc giữa hai vecto trong không gian

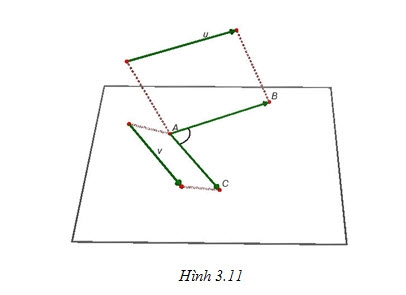
Định nghĩa: Trong không gian, cho và $\overrightarrow{v}$ là hai vecto khác vecto- không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho $\overrightarrow{AB}=\overrightarrow{u},\overrightarrow{AC}=\overrightarrow{v}$. Khi đó ta gọi góc $\widehat{BAC}$ $(0^0\leq \widehat{BAC}\leq 180^0)$ là góc giữa hai vecto và $\overrightarrow{v}$ trong không gian, kí hiệu là: $\left ( \overrightarrow{u},\overrightarrow{v} \right )$ (Hình 3.11)

2. Tích vô hướng của hai vecto trong không gian

Định nghĩa: Trong không gian, cho và $\overrightarrow{v}$ là hai vecto khác vecto- không. Tích vô hướng của hai vecto và $\overrightarrow{v}$ là một số, kí hiệu là: $\overrightarrow{u}.\overrightarrow{v}$, được xác định bởi công thức sau:

II. VECTO CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG

1. Định nghĩa

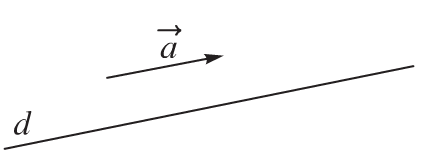
Vecto khác vecto- không được gọi là vecto chỉ phương của đường thẳng $d$ nếu giá của vecto song song hoặc trùng với đường thẳng $d$.

2. Nhận xét

a) Nếu là vecto chỉ phương của đường thẳng $d$ thì vecto $k\overrightarrow{a}$ với $k\neq 0$ cùng là vecto chỉ phương của $d$.

b) Một đường thẳng trong không gian hoàn toàn được xác định nếu biết một điểm $A$ thuộc và một vecto chỉ phương $\overrightarrow{a}$ của nó.

c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vecto chỉ phương cùng phương.

III. GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN

1. Định nghĩa

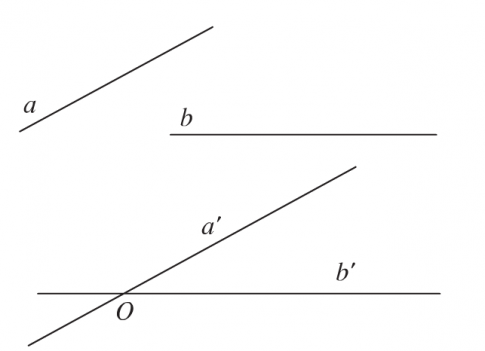
Góc giữa hai đường thẳng và $b$ trong không gian là góc giữa hai đường thẳng $a'$ và $b'$ cùng đi qua một điểm và lần lượt song song với và $b$.

2. Nhận xét

a) Để xác định góc giữa hai đường thẳng và $b$ ta có thể lấy điểm $O$ thuộc một trong hai đường thẳng đó rồi vẽ đường thẳng qua $O$ và song song với đường thẳng còn lại.

b) Nếu là vecto chỉ phương của đường thẳng $a$ và $\overrightarrow{v}$ là vecto chỉ phương của đường thẳng $b$ và $\left ( \overrightarrow{u},\overrightarrow{v} \right )=\alpha $ thì góc giữa hai đường thẳng $a$ và $b$ bằng $\alpha $ nếu $0^0\leq \alpha \leq 90^0$ và bằng $180^0-\alpha $ nếu $90^0\leq \alpha \leq 180^0$.

Nếu và $b$ song song với nhau thì góc giữa chúng bằng $0^0$.

IV. HAI ĐƯỜNG THẲNG VUÔNG GÓC

1. Định nghĩa

Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng .

2. Nhận xét

a) Nếu là vecto chỉ phương của đường thẳng $a$ và $\overrightarrow{v}$ là vecto chỉ phương của đường thẳng $b$ thì;

b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với một trong hai đường thẳng đã cho thì vuông góc với đường thẳng còn lại.

c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.