Giải câu 3 bài 3: Đường thẳng và mặt phẳng song song

Câu 3: Trang 63 - SGK hình học 11

Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) đi qua O, song song với AB và SC. Thiết diện đó là hình gì ?

Bài làm:

Theo giả thiết ta có hình vẽ sau:

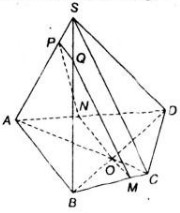
Ta có:

• (α) // AB
• AB ⊂ (ABCD),
• O là điểm chung của (α) và (ABCD)

=> ( α) ∩ (ABCD) = MN qua O và song song với AB.

Chứng minh tương tư ta được

• ( α) ∩ (ABCD) = PQ qua O và song song với AB.
• ( α) ∩ (ABCD) = PN qua O và song song với SC.
• ( α) ∩ (ABCD) = QM qua O và song song với SC.

Vậy thiết diện là hình hành MNPQ.