Giải câu 4 bài 1: Giá trị lượng giác của một góc bất kì

Câu 4: Trang 40 - sgk hình học 10

Chứng minh rằng với mọi góc $\alpha$ $(0^{\circ}\leq \alpha \leq 180^{\circ})$ ta đều có $\cos ^{2}\alpha +\sin ^{2}\alpha =1$.

Bài làm:

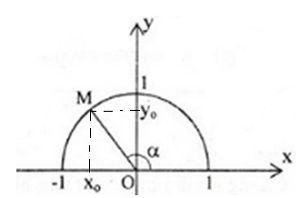
Hướng dẫn giải câu 4 bài Giá trị lượng giác của một góc bất kì

Vẽ đường tròn lượng giác $C(O; 1)$ . Theo định nghĩa, điểm $M(x_{0}; y_{0})$ thuộc đường tròn có:

$\sin \alpha =y_{0}$

$\cos \alpha =x_{0}$

Áp dụng định lí Pitago ta có:

$x_{0}^{2}+y_{0}^{2}=OM^{2}=1$

<=> $\cos ^{2}\alpha +\sin ^{2}\alpha =1$ . (đpcm)

Cập nhật: 07/09/2021

Xem thêm bài viết khác