Giải câu 16 bài: Luyện tập sgk Toán Hình 8 tập 1 Trang 75

Câu 16: Trang 75- sgk toán 8 tập 1

Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Bài làm:

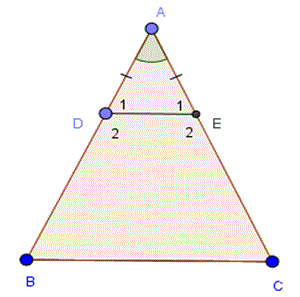
a) Xét ΔABD và ΔACE có :

• AB = AC (gt)
• chung
• 

=> ΔABD = ΔACE ( g-c-g )

=> AD = AE .

=> ΔADE cân .

=>

Xét , ta có : $\widehat{E_{1}}+\widehat{D_{1}}+\widehat{A}=180^{\circ}$

<=>

=>

Xét , ta có : $\widehat{B}=\frac{180^{\circ}-\widehat{A}}{2}$

=> ( hai góc đồng vị )

=> DE // BC

=> DEBC là hình thang .

Mặt khác , ta có :

=> DEBC là hình thang cân.

=> DE // BC.

=> ( so le trong )

Mà:

=> ΔEBD cân => EB = ED.

Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên. ( đpcm )