Giải câu 65 bài: Luyện tập sgk Toán hình 8 tập 1 Trang 100

Câu 65 : Trang 100 sgk toán 8 tập 1

Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?

Bài làm:

Theo giả thiết ta có hình vẽ sau:

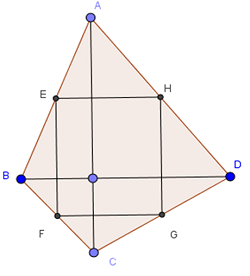
Do E là trung điểm của AB và F là trung điểm của BC

=>EF là đường trung bình của ∆ABC => EF // AC và EF = AC (1)

Với H và G lần lượt là trung điểm của AD và DC, chứng minh tương tự

=>HG // AC và HG = AC (2)

Từ (1) và (2) => FE // HG và FE = HG = AC

=> EFGH là hình bình hành.

Ta có : EF // AC (cmt) và BD ⊥ AC (gt) => BD ⊥ EF

Mặt khác ta có EH // BD và EF ⊥ BD => EF ⊥ EH hay = 90⁰

Hình bình hành EFGH có = 90⁰ nên là hình chữ nhật.