Dạng 1: Tính diện tích hình phẳng giới hạn bởi hai đường y=f(x) và y=g(x).

Phần tham khảo mở rộng

Dạng 1: Tính diện tích hình phẳng giới hạn bởi hai đường y=f(x) và y=g(x).

Bài làm:

I.Phương pháp giải

Ta tìm hoành độ giao điểm của hai đường từ phương trình: f(x) - g(x) = 0.

Lập bảng xét dấu của hàm số f(x)-g(x) trên [a; b] trong đó a, b là nghiệm nhỏ nhất và lớn nhất của phương trình f(x) - g(x) = 0.

Dựa vào bảng xét dấu tính tích phân .

II.Bài tập vận dụng

Bài tập 1: Tính diện tích hình phẳng giới hạn bởi các đường thẳng .

Bài giải:

Ta đặt

Ta có: hoặc $x=2$

Dó đó diện tích cần tính là:

.

Bài tập 2: Tính diện tích các hình phẳng giới hạn bởi các đường .

Bài giải:

Đặt .

hoặc $x=2$ hoặc $x=3$.

Ta có bảng xét dấu:

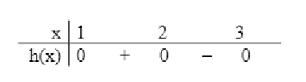
Từ bảng xét dấu ta có diện tích cần tính là:

- $\int_{2}^{3}(x^3-6x^2+11x-6)dx$