Dạng 2: Tìm thể tích khối tròn xoay được giới hạn bởi đồ thị các hàm số y=f(x), y=g(x), y=h(x).

Dạng 2: Tìm thể tích khối tròn xoay được giới hạn bởi đồ thị các hàm số y=f(x), y=g(x), y=h(x).

Bài làm:

I.Phương pháp giải

Ta tính các giao điểm a, b, c là nghiệm của các phương trình f(x)=g(x), g(x)=h(x), h(x)=f(x)..

Ta áp dụng công thức:

II.Bài tập vận dụng

Bài tập 1: Cho miền D giới hạn bởi đồ thị (C): . Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox.

Bài giải

Ta tìm giao điểm của các đường đã cho:

do $x\geq 0$

vì $x\geq 0$.

Do đó :

Bài tập 2: Cho miền D giới hạn bởi đồ thị các đường . Tính thể tích khổi tròn xoay được tạo nên khi D xoay quanh trục Oy.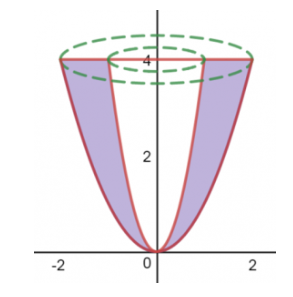

Bài giải

Ta chuyển đổi hàm số:

Ta có: .

Vì đồ thị hai đường giao nhau tại O nên ta có thể tích cần tính là:

=π$\left | \int_{0}^{4}\left ( (\sqrt{y})^{2}-(\frac{\sqrt{y}}{2})^{2} \right )dy \right |$

=4π (đvtt)