Giải Câu 27 Bài 4: Tính chất ba đường trung tuyến của tam giác sgk Toán 7 tập 2 trang 67

Câu 27: Trang 67 - SGK Toán 7 tập 2

Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Bài làm:

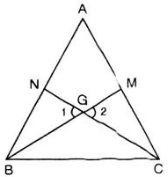
Vẽ ΔABC. Gọi M, N lần lượt là trung điểm của AC và AB và gọi G là trọng tâm của tam giác.

Theo đề bài: CN = BM.

Vì G là trọng tâm tam giác ABC nên: CG = CN; BG = BM.

Suy ra: CG = BG.

Ta có: NG = CN - CG = BM - BG = GM.

Xét tam giác BGN và CGM có:

CG = BG (cmt)

(đối đỉnh)

NG = GM (cmt)

Mà M, N là trung điểm AB, AC nên AB = AC.

Vậy tam giác ABC cân tại A.