Giải câu 65 bài: Luyện tập sgk Toán 7 tập 1 Trang 137

Câu 65 : Trang 137 - sgk toán 7 tập 1

Các tam giác ABC cân tại A ( < 90⁰). Vẽ BH ⊥ A (H thuộc AC), CK ⊥ AB (K thuộc AB)

a) Chứng minh rằng AH = AK.

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng tia AI là tia phân giác của góc A.

Bài làm:

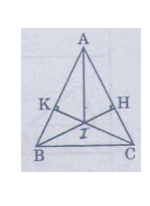
Do tam giác ABC cân tại A => AB = AC

a) Xét tam giác vuông ABH và tam giác vuông ACK có:

AB = AC (chứng minh trên)

Góc A chung.

=> ∆ABH = ∆ACK (cạnh huyền - góc nhọn)

=> AH = AK (cạnh tương ứng) (đpcm)

b) Xét tam giác vuông AIK và tam giác AIH có:

AK = AH (cmt)

AI cạnh chung

=> ∆AIK = ∆AIH (cạnh huyền- cạnh góc vuông)

=> = \(\widehat{IAH}\)

=> AI là tia phân giác của góc A. (đpcm)