Dạng 3: Xét dấu các hệ số của hàm bậc nhất trên bậc nhất, phân tích đồ thị hàm số.
Dạng 3: Xét dấu các hệ số của hàm bậc nhất trên bậc nhất, phân tích đồ thị hàm số.
Bài làm:
I.Phương pháp giải
Xét đồ thị hàm số ![]() ($c\neq 0, ad-cb\neq 0$). Ta có:
($c\neq 0, ad-cb\neq 0$). Ta có:
a) Đồ thị có TCN là đường thẳng ![]() .
.
- TCN nằm phía trên trục hoành
 .
. - TCN nằm phía dưới trục hoành
 .
. - TCN là trục hoành
 .
.
b) Đồ thị có TCĐ là đường thẳng ![]() .
.
- TCĐ nằm bên phải trục tung
 ;
; - TCĐ nằm bên trái trục tung
 ;
; - TCĐ là trục tung
 .
.
c) Giao điểm của đồ thị với trục tung là điểm ![]() :
:
- M nằm phía trên trục hoành
 ;
; - M nằm phía dưới trục hoành
 ;
; - M nằm thuộc trục hoành
 .
.
II.Bài tập vận dụng
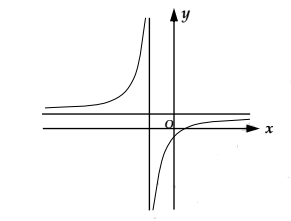
Bài tập 1: Hàm số ![]() ($c\neq 0, ad-bc\neq 0$) có đồ thị như hình vẽ.
($c\neq 0, ad-bc\neq 0$) có đồ thị như hình vẽ.
Chứng minh ![]() .
.
Bài giải:
Nhìn vào đồ thị ta thấy:
- Đồ thị có TCN là đường thẳng
 , đường thằng này nằm phía trên trục hoành $\Leftrightarrow \frac{a}{c}>0\Leftrightarrow a.c>0$.
, đường thằng này nằm phía trên trục hoành $\Leftrightarrow \frac{a}{c}>0\Leftrightarrow a.c>0$. - Đồ thị có TCĐ là đường thẳng
 , đường thẳng nằm bên trái trục tung $\Leftrightarrow \frac{-d}{c}<0 \leftrightarrow d.c>0$.
, đường thẳng nằm bên trái trục tung $\Leftrightarrow \frac{-d}{c}<0 \leftrightarrow d.c>0$. - Giao điểm của đồ thị với trục tung nằm bên dưới trục hoành
 .
.
Ta chọn a > 0 nên suy ra  . Do đó $\left\{\begin{matrix}ad>0\\ bc
. Do đó $\left\{\begin{matrix}ad>0\\ bc
Bài tập 2: Hàm số ![]() ($c\neq 0, ad-bc\neq 0$) có đồ thị như hình vẽ.
($c\neq 0, ad-bc\neq 0$) có đồ thị như hình vẽ.
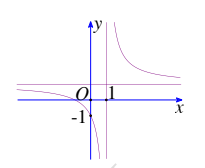
Xác định dấu của ad, bc.
Bài giải:
Nhìn vào đồ thị ta thấy:
- Đồ thị có TCN là đường thẳng
 , đường thằng này nằm phía trên trục hoành $\Leftrightarrow \frac{a}{c}>0\Leftrightarrow a.c>0$.
, đường thằng này nằm phía trên trục hoành $\Leftrightarrow \frac{a}{c}>0\Leftrightarrow a.c>0$. - Đồ thị có TCĐ là đường thẳng
 , đường thẳng nằm bên phải trục tung $\Leftrightarrow \frac{-d}{c}>0\Leftrightarrow d.c
, đường thẳng nằm bên phải trục tung $\Leftrightarrow \frac{-d}{c}>0\Leftrightarrow d.c - Giao điểm của đồ thị với trục tung nằm bên dưới trục hoành
 .
.
Ta chọn a > 0 nên suy ra  . Do đó $ad<0 ; bc>0$ .
. Do đó $ad<0 ; bc>0$ .
Xem thêm bài viết khác
- Giải bài 4: Đường tiệm cận
- Giải câu 6 bài: Ôn tập chương 4
- Giải câu 1 bài: Ôn tập chương 4
- Giải câu 5 bài: Tích phân
- Giải bài 5: Phương trình mũ. Phương trình Lôgarit
- Giải câu 4 bài: Phương trình mũ. Phương trình Lôgarit
- Giải bài 4: Hàm số mũ. Hàm số Lôgarit
- Dạng 4: Tính đơn điệu của hàm hợp
- Giải câu 5 bài: Hàm số mũ. Hàm số Lôgarit
- Giải câu 3 bài: Lũy thừa
- Giải bài 1: Nguyên hàm
- Giải câu 1 bài 1: Sự đồng biến, nghịch biến của hàm số











