Dạng 1: Xét dấu các hệ số của hàm bậc bốn trùng phương, phân tích đồ thị hàm số.

Phần tham khảo mở rộng

Dạng 1: Xét dấu các hệ số của hàm bậc bốn trùng phương, phân tích đồ thị hàm số.

Bài làm:

I.Phương pháp giải

Xét đồ thị hàm số ($a\neq 0$).

1. Xác định dấu của a

Từ đồ thị, ta tìm được giới hạn . Ta có:

• .
• .

2. Xác định dấu của b

• Đồ thị có ba điểm cực trị .
• Đồ thị có một điểm cực trị .

3. Xác định dấu của c

Ta có M(0; c) là giao điểm của đồ thị với trục tung, suy ra:

• Nếu M nằm phía trên trục hoành .
• Nếu M nằm phía dưới trục hoành .
• Nếu M thuộc trục hoành .

II.Bài tập vận dụng

Bài tập 1: Đồ thị hàm số ($a\neq 0$) có dạng sau:

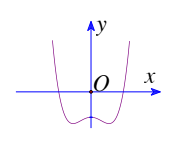
Xác định dấu của a, b, c

Bài giải:

Hàm số là hàm trùng phương, có .

Đồ thị hàm số có ba điểm cực trị nên a.b < 0. Mà a > 0 do đó b < 0.

Đồ thị hàm số cắt trục tung tại điểm nằm bên dưới trục hoành, do đó c < 0.

Vậy a > 0; b < 0; c < 0.

Bài tập 2: Đồ thị hàm số ($a\neq 0$) có dạng sau:

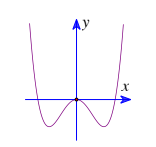
Xác định dấu của a, b, c.

Bài giải:

Ta có:

Hàm số là hàm trùng phương, có .

Đồ thị hàm số có ba điểm cực trị nên a.b < 0. Mà a > 0 do đó b < 0.

Đồ thị hàm số cắt trục tung tại điểm thuộc trục hoành, do đó c = 0.

Vậy a > 0; b < 0; c = 0.